GpSense:一种用于在常识知识库中进行子图匹配的方法
Section2:基于“过滤和合并”(filtering-and-joining)策略的并行计算架构
- 子图同构:在大图中寻找一个与特定结构的小图相匹配的子图
- 子图匹配:找出所有的同构子图

generate_query_plan(q, g):为后续的搜索任务创建一个良好的节点顺序。首先选择的节点应该是有助于最小化查询节点和边的候选集合的大小。节点的排序规则 $f(u)=deg(u)/freq(u.label)$。deg(u) 是查询节点 u 的度,freq(u.label) 是与节点 u 有相同标签的数据图节点的数量。该函数更趋向于度数高、频率低的节点。选定第一个节点之后,generate_query_plan 会继续访问其邻居以找到下一个还未被选择并且至少连接了一个在节点序列中节点的节点,直到所有查询节点被选中该过程终止。
Filtering Phase:该部分的目的就是减少节点候选集的数量,从而减少边的候选集的数量以及joining phase的运行时间。该阶段包含两个任务:初始化节点候选集合以及精简节点候选集合。
Joining Phase:基于查询节点的候选集,collect_edge_candidates函数会单独地收集候选边。combine_edge_candidates 合并侯选边以生成最后的子图匹配结果。
Section3:将常识知识库转换为有向图
通过将三元组 <concept-relation-concept> 当作有向带权图的边,知识库自然就转换成了有向图,即将概念(concept)映射成节点,将关系(relation)映射成边的权值或标签。获得有向图之后就可以将每个节点标签转换为唯一的节点ID。
Section4:GPU实现细节
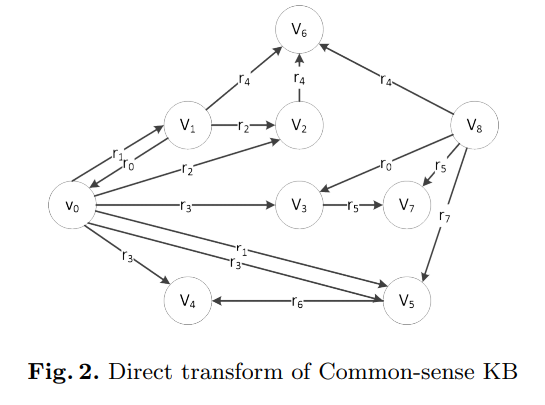
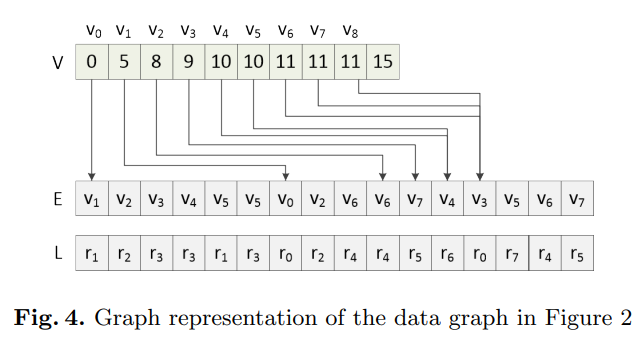
图表示的数据结构(三个数组):
- 节点数组|V|:数组长度为节点个数加 1
- 边数组|E|:由 |V| 中所有节点的邻接表组成节点数组中的节点指向边数组中节点的邻接表。此外节点数组的最后一个元素表述边数组的长度。
- 第三个数组:与边数组 |E| 的长度相同,存储数据图中所有边的标签。
这种数据结构的优势在于,节点邻接表中的节点彼此相邻存储在GPU内存中。在GPU执行期间,连续的线程可以访问内存中的连续元素。 因此可以避免随机访问问题,从而减少基于GPU的方法的访问时间。
GPU 实现,介绍 Algorithm 1 中的一些函数,这些函数都基于两个优化技巧:占用率最大化,以隐藏内存访问延迟;基于wrap的执行方式,以利用合并(coalesce)的访问并处理 wrap中线程之间的工作负载不平衡。
优化技巧:
Use both incoming and outgoing graph representations. Consequently, GpSense can reduce a large amount of intermediate results during execution which is one of the most crucial issues for GPU applications
同时使用传入和传出图形表示。 因此,GpSense可以减少执行期间的大量中间结果,这是GPU应用程序最关键的问题之一
Section5:实现结果
- 数据集:
- 数据图:SenticNet 及其扩展
- 查询图:从数据图中抽取节点并用BFS的方式扩展(从 SenticNet的密集区域抽取以确保查询结果不会只有“树”型)
- 用于比较的算法:VF2、QuickSI (QSI)、GraphQL (GQL)、TurboISO
- 验环境:
- CPU:Intel Core i7-870 2.93GHz / 8GB RAM
- GPU:NVIDIA Tesla C2050 / 3GB global memory / 48KB shared memory
- CUDA toolkit: 6.0
各算法执行100次不同的查询并记录平均耗时(average elapsed time)
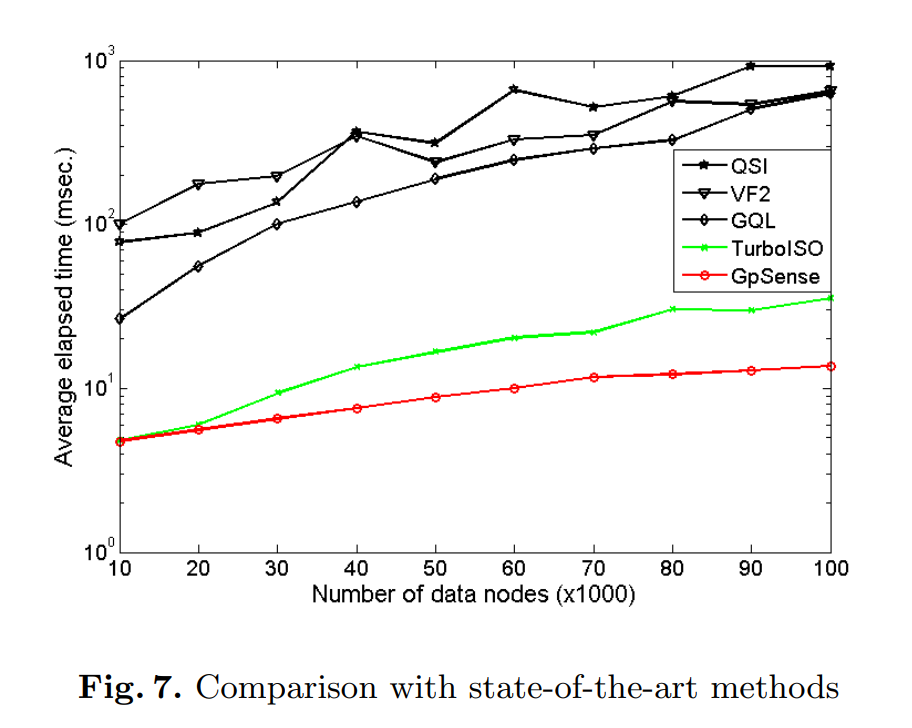
TurboISO算法与GpSense算法在10000个节点上的查询性能类似,但是当数据图规模不断增大时,GpSense算法的性能要优于TurboISO算法。将这两个算法进一步进行对比,分别测试查询图的节点数以及平均节点度数对两个算法效率的影响:
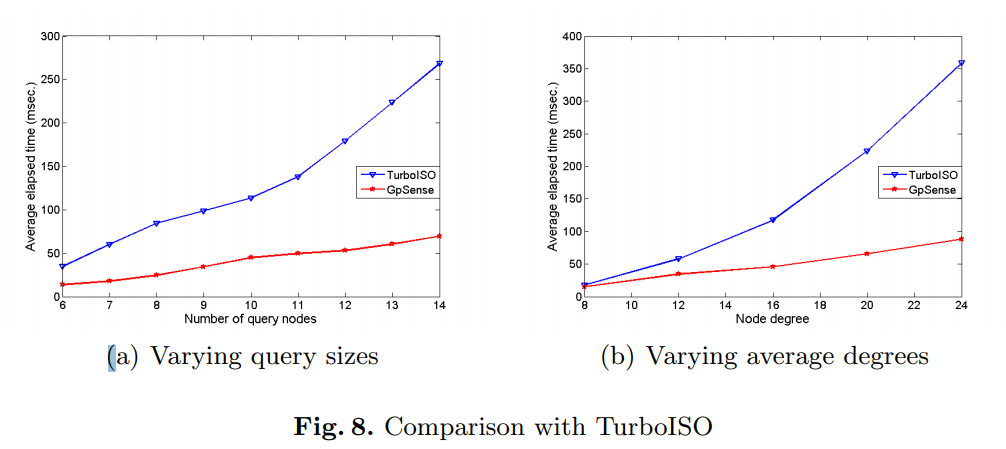
TurboISO的递归调用次数相对于查询图的大小和数据图的程度呈指数增长。相反,具有大量并行线程的GpSense可以同时处理多个候选节点和边,因此,GpSense的性能更趋于稳定。
Section6:结论
提出了一种高效的适用于GPU的用于大规模常识知识库的子图匹配查询方法。该方法基于过滤与合并(“filtering-and-joining”)的策略。最终的实验结果表明该方法优于基于CPU的回溯算法。